Интерпретация модели в условиях найма на рынке труда

Рассмотрим следующую задачу со следующими предположениями:

1) функция полезности агента вогнута и имеет вид [4];

) агент может выбрать нулевой уровень усилий, либо уровень усилий e;

) - альтернативный уровень полезности агента внутри рынка (то есть уровень полезности, который агент может получить, выбрав другого работодателя);

) вероятности получения высокого или низкого уровня выпуска фирмы при различном уровне усилий агента описаны в таблице 1.

Таблица 1 - Вероятность получения различного уровня выпуска фирмы в зависимости от усилий работника

Замечание: логично предположить, что p1>1- p1, так как ясно, что при нулевых усилиях гораздо вероятнее получение низкого уровня прибыли, чем высокого. Аналогично, для высокого уровня усилий p2>1- p2. Таким образом, получим, что

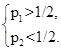
Решение

1. Случай наблюдаемости усилий

В случае, когда усилия наблюдаемы, работодатель может явно оценить усилия агента. Таким образом, в этом случае доход компании зависит от усилий агента в явной форме:

Работодатель пытается подобрать контракт, стимулирующий высокий уровень усилий. Условие участия тогда будет выглядеть так:

Тогда ожидаемый доход равен

Ожидаемая чистая прибыль:

В условиях наблюдаемости усилий можно рассмотреть следующие случаи:

1) Случай, когда количество агентов ограничено (много принципалов - один агент);

а) в случае, когда принципалу выгодно, чтобы работник выбирал высокий уровень усилий e, получим задачу максимизации с ограничениями-неравенствами:

(1)

Очевидно, что в случае конкуренции принципалов, каждый из них получит нулевую чистую прибыль (условие совершенной конкуренции). В данной ситуации это будет объясняться тем, что каждый работодатель готов платить агенту максимально возможную зарплату, чтобы единственный на рынке агент не желал поменять место работы.

В этом случае получим: . Тогда полезность агента будет равна:

.

Таким образом, если выполнено второе неравенство системы (1), то заработная плата, стимулирующая высокий уровень усилий, равна . Но всегда ли выполнено неравенство (1)? Проверим это, выразив вероятность p2:

.

Ясно, что . Тогда, если , то неравенство всегда верно (так как вероятность всегда больше отрицательного числа), однако, в силу ограничения неотрицательности на чистую прибыль, такого быть не может.

Если же числитель больше знаменателя, , то система не имеет решения (вероятность не может быть больше единицы), и агент предпочтет уйти к другому работодателю.

б) Случай, когда принципалу выгоден нулевой уровень усилий агента, приводит к следующей задаче с ограничениями:

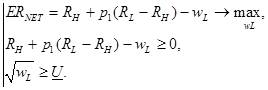
Тогда, проводя рассуждения, аналогичные случаю а), получим:

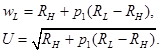
Немного больше по теме

Политика занятости в современной России
Занятость является одной из существенных характеристик экономики, благосостояния народа. Уровень занятости представляет собой важнейший макроэкономический показатель. Но занятость не чистое экономическое явление. Она обусловлена демографическими процессами, выступает частью социальной политики, т.е. имеет демографическое и социальное содержание. Как экономическая категория, заня ...