Корреляционно-регрессионный анализ

Выясним, существует ли связь между исследуемыми признаками графическим способом. Для этого представим данные зависимости на графике (рис. 8.1 и 8.2) и добавим линию тренда. На графике видно, что между исследуемыми показателями существует прямо пропорциональная связь, т.е. с увеличением числа расходов растут и доходы Калужской области.

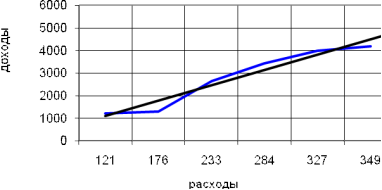
Рис. 8.1. График зависимости доходов Калужской области от расходов

Зависимость между доходами и расходами имеет линейный характер и выражена обратной функцией.

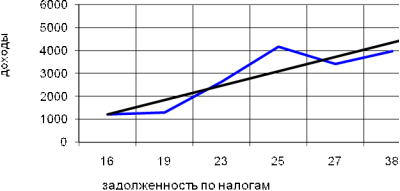
Рис. 8.2. График зависимости доходов Калужской области от задолженности по налогам

График зависимости линейный, так как график состоит из ломаной линии. Выясним обратная она или нет аналитически.

График зависимости представляет собой линейную функцию вида .

Система уравнений для данного исследования будет иметь вид:

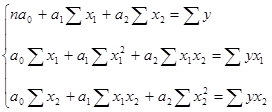
Система уравнений примет вид:

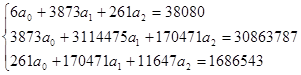
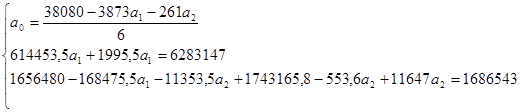
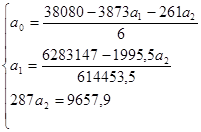
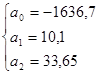
Рассчитаем частные коэффициенты эластичности, которые используются с целью расширения возможностей экономического анализа. Они находятся по следующей формуле:

, (8.1)

где - коэффициент регрессии при соответствующем факторном признаке; - среднее значение соответствующего факторного признака; - среднее значение результативного признака, которые находятся по формулам:

, (8.2)

(8.3)

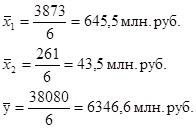
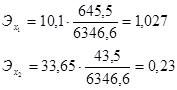
Это значит, что при увеличении числа расходов на 1%, число доходов Калужской области увеличится на 1,027%, а при увеличении задолженности по налогам на 1% доходы увеличатся на 0,23%.

Рассчитаем частные коэффициенты детерминации по формуле

, (8.4)

где - парный коэффициент корреляции между результативным и -м факторным признаками; - соответствующий коэффициент уравнения множественной регрессии в стандартизированном масштабе.

Парный коэффициент корреляции находится по формуле:

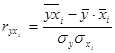(8.5)

Рассчитаем парный коэффициент корреляции между результативным и первым факторным признаками, т.е. между доходами и расходами.

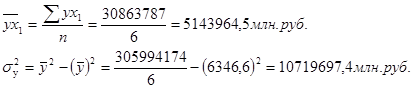
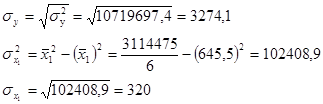
. Т.е. связь между признаками прямая и однонаправленная.

Рассчитаем парный коэффициент корреляции между результативным и вторым факторным (задолженности по налогам) признаками.

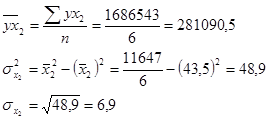
. Значение коэффициента говорит о том, что между признаками существует прямая связь.

Найдем -коэффициент по формуле:

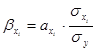, (8.6)

где - среднее квадратическое отклонение -го фактора; - среднее квадратическое отклонение результативного признака.

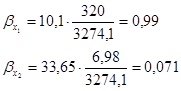
Тогда частные коэффициенты детерминации составят:

Из этого следует, что на 98% вариация доходов Калужской области объясняется изменением числа расходов, и 1,6% вариации - изменением задолженности по налогам в бюджет.

Найдем - коэффициент по формуле:

= V, (8.7)

Немного больше по теме

Повышение эффективности деятельности предприятия в рыночных условиях (на примере ООО Дабан)
На современном этапе хозяйствования основой экономической политики является повышение эффективности и качества работы всех звеньев промышленного производства. Развитие рыночных отношений повышает ответственность и самостоятельность предприятий всех форм собственности в выработке управленческих решений по обеспечению эффективности их производственно-хозяйственной деятельности. Дейс ...