Проверка основной гипотезы

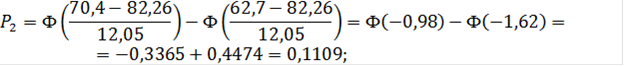
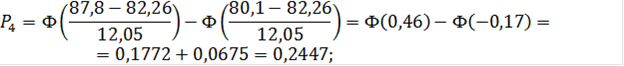
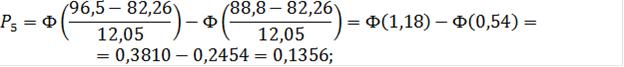
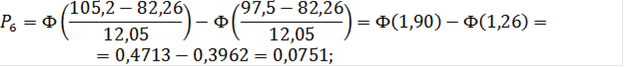
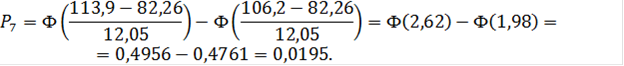
Для того чтобы соблюсти условие , объединим в один 1,7,8 интервалы.

В этом случае после подстановки конкретных значений в выражение

Получим,

Для второго интервала:

Для третьего интервала:

Для четвёртого интервала:

Для пятого интервала:

Для шестого интервала:

Суммируем все значения и определяем

При числе степеней свободы , имеем и табличное значение критерия Пирсона (см. таблицу 3 приложения).

Отсюда

Следовательно, по критерию Пирсона следует отклонить основную гипотезу.

Немного больше по теме

Последствия безработицы и основные направления ее регулирования
Актуальность исследования обусловлена тем, что в современных условиях занятость и труд, качество и состояние экономически активного населения являются важнейшими факторами устойчивого поступательного движения экономики. Показатели занятости и безработицы входят в число ключевых макроэкономических показателей, на основании которых оцениваются существующие тенденции и перспективы ро ...