Расширение модели ненаблюдаемых действий

Как правило, в реальности используются линейные или кусочно-линейные зависимости. Типичный пример: поведение менеджера-собственника фирмы, находящейся на грани банкротства. До того как долговое бремя стало чрезмерным, стимулы собственника были фактически линейными: каждый дополнительный доллар прибыли доставался ему (выплаты по долгу, по определению, фиксированы). Однако, как только менеджер начинает понимать, что вероятность банкротства становится существенной, его «контракт» становится выпуклым: если банкротства не произойдет (прибыли превысят необходимые долговые выплаты), то он по-прежнему получает каждый дополнительный доллар, если же прибыль ниже необходимых выплат по долгу, он получает ноль, и каждый дополнительный доллар достается кредиторам. Естественно, искаженные (нелинейные) стимулы приводят к тому, что менеджер предпринимает очень рискованные (и не обязательно прибыльные) проекты: он получает выигрыш в случае положительного исхода, но не заботится о проигрыше в случае отрицательного исхода.

Для того, чтобы смоделировать такого рода соображения, Holmstrom и Milgrom предложили следующую модификацию изложенной выше модели [5]. Доход принципала по-прежнему зависит от усилий агента и внешних (случайных воздействий), однако вместо одномоментного соотношения x = a+ε рассмотрим динамику выбора усилий и случайных факторов в течение данного периода t ∈ [0, 1]. Предположим, что доход накапливается со временем по закону dx = adt + σdW, где a(t) - уровень усилий в момент времени t, а W - винеровский случайный процесс (иначе говоря, единичное броуновское случайное блуждание). За время dt приращение винеровского процесса dW - это нормально распределенная случайная величина со средним 0 и дисперсией dt (среднеквадратичное отклонение равно √dt). Таким образом, в конце периода

, где ε ∈ N(0, σ2).

Положим x(0) = 0 и введем обозначение для среднего уровня усилий:

.

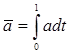Тогда в конце периода доход принципала равен среднему уровню усилий плюс нормально распределенная случайная величина: x(1) = + ε. Следующее предположение заключается в том, что принципал наблюдает x только в конце периода (например, получает годовой отчет, но не может следить за ежедневными результатами деятельности агента) [5].

Отличи от стандартной постановки: в данном случае агент выбирает уровень усилий в промежуточные моменты времени, зная реализацию случайных факторов к данному моменту. Поэтому, выбор a(t) существенно зависит от наблюдаемой им (но не принципалом) величины x(t): если агент знает, что в предыдущие момент времени ему повезло, то его шансы добиться более высоких результатов в конце периода выше (даже при том же уровне усилий). Поэтому агент будет ориентироваться на ту часть контракта w(x(1)), которая оговаривает зарплату в случае высоких результатов. Если же агенту не повезло и величина x(t) не так велика, то более вероятны низкие значения x(1), и он будет скорее рассматривать ту часть контракта w(x(1)), которая определяет платежи в случае плохих результатов.

Как и в предыдущей модели, агент получает нулевую ренту, поэтому максимизация выигрыша принципала соответствует задаче максимизации общего благосостояния. С этой же точки зрения, гибкость - это плохо. Действительно, агент боится риска, поэтому, если его усилия будут меняться в зависимости от промежуточных реализаций случайных величин, принципалу придется повысить его среднюю зарплату в качестве компенсации за риск. Следовательно, принципал заинтересован в том, чтобы агент выбирал один и тот же уровень усилия. Этого можно добиться тогда и только тогда, когда предельные стимулы, предоставляемые контрактом, не будут зависеть от реализации случайных величин. Другими словами, у линейного контракта w(x(1)) = αx(1) + β есть серьезные преимущества.и Milgrom доказывают оптимальность линейных контрактов для следующего примера. Принципал нейтрален к риску, а агент обладает постоянной абсолютной несклонностью к риску r, то есть его функция полезности CARA (constant absolute risk aversion): u(w) = 1 − e−r(w−c(a)). Для простоты предположим, что функция издержек от усилий c(a) = a2/2.

Даже для этой постановки доказательство оказывается достаточно сложным, поэтому мы не будем его обсуждать, но рассмотрим оптимальный контракт.

В равновесии агент получает линейный контракт w(x(1)) = αx(1) + β и выбирает один и тот же уровень усилий a(t) = a в каждый момент времени. Чтобы вычислить оптимальные параметры α, β, необходимо вернуться к исходной (статической постановке) и решить задачу об оптимальном контракте при ограничении линейности контракта. Другими словами, необходимо искать не оптимальный контракт в общем виде, а всего лишь максимизировать по α, β. Ограничения индивидуальной рациональности и совместимости по стимулам имеют следующий вид:

Немного больше по теме

Прибыль фирмы
В условиях трансформируемой экономики, в процессе перехода к инновационной экономике роль прибыли фирмы возрастает. Особенность формирования, а также распределения прибыли, в том числе на инновационную деятельность, определяется целями фирмы, адекватной современному этапу развития. В связи с этим возросла и актуальность изучения проблемы экономической природы прибыли. Прибы ...