Определение показателей вариации

Любая статистическая совокупность состоит из единиц, значения признака которых варьируют. Для того, чтобы судить об однородности совокупности и типичности средней величины изучаемого признака, анализ следует дополнять исчислением показателей вариации.

Вариация - это колеблемость, многообразие, изменяемость величины признака у отдельных единиц совокупности.

К абсолютным показателям вариации относят: размах вариации, среднее линейное отклонение, дисперсию и среднее квадратическое отклонение.

Размах вариации - характеристика границ вариации изучаемого признака. Показывает, сколь велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признака, основан на крайних значениях варьирующего признака и не отражает отклонений всех вариант в ряду. Определяется по формуле:

=Xmax-Xmin, (5.4)

где Xmax - максимальное значение вариационного ряда;

Xmin - минимальное.

Среднее линейное отклонение показывает, на какую величину отклоняется признак в изучаемой совокупности от средней величины признака. Находится по формуле:

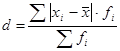, (5.5)

где - индивидуальные значения варьирующего признака (варианты); - частоты, веса; - среднее значение варьирующего признака;

Дисперсия - средний квадрат отклонения индивидуальных значений признака от их средней величины. Вычисляется по следующим формулам.

Первый способ определения дисперсии:

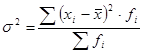, (5.6)

Второй способ определения дисперсии (по средней арифметической):

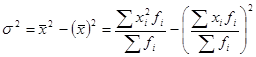, (5.7)

где - средняя из квадратов индивидуальных значений; - квадрат средней величины признака.

Среднее квадратическое отклонение - это обобщающая характеристика размеров вариации признака в совокупности. Показывает, на какую величину в среднем значение признака отличается от стандартного значения, определяется по формуле:

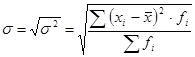. (5.8)

Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее (количественно) совокупность и тем более типичной будет средняя величина.

Рассчитаем показатели вариации для группировки транспортных организаций по грузообороту автомобильного транспорта (таблица 5.1).

Найдем размах вариации (по формуле 5.4):

Разброс значений грузооборота транспорта общественного пользования достаточно высок.

Вычислим среднее линейное отклонение (по формуле 5.5):

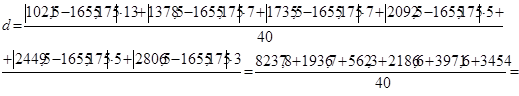
Значения грузооборота автомобильного транспорта отличались от среднего значения на 508,8 млн. т. км.

Рассчитаем дисперсию двумя способами (по формулам 5.6 - 5.7). Первый способ:

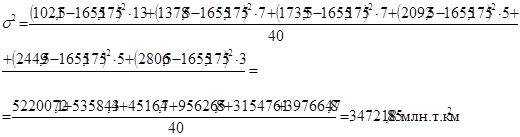
Второй способ (по средней арифметической):

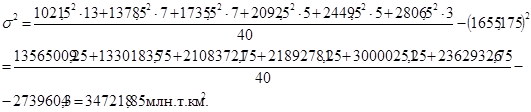
Вычислим среднее квадратическое отклонение (по формуле 5.8):

Немного больше по теме

Прибыль и рентабельность организации сферы услуг резервы и пути их роста
Рыночные отношения в экономике Республики Беларусь расширяют возможности деятельности организации, как основного ее звена. В новых условиях существенно поменялись правовые, финансово-экономические и социальные отношения как внутри организации, так и во внешней среде. Сложилось многообразие форм собственности; существенно изменились отношения организаций с государством и другими с ...